4.3 Crout’s LU Factorization
An equivalent LU decomposition of A = LU may be obtained by assuming that L is lower triangular and U is unit upper triangular. This factorization scheme is referred to as Crout’s method. The defining equations for Crout’s method are
| $$l_{ij}=a_{ij}-\displaystyle\sum_{p=1}^{i-1}l_{ip}u_{pj},\mbox{ where }i \geq j$$ | (49) |
and
| $$u_{ij}=\frac{a_{ij}-\displaystyle\sum_{p=1}^{i-1}l_{ip}u_{pj}}{l_{ii}},\mbox{ where }i \lt j$$ | (50) |
Algorithm 3 implements Crout’s method. Calculations are sequenced to compute one column of L followed by the corresponding row of U until A is exhausted.
| for $j=1,\cdots,n$ |
| for $i=j,\cdots,n$ |
| $\alpha=a_{ij}$ |
| for $=1,\cdots,j-1$ |
| $\alpha=\alpha-a_{ip}a_{pj}$ |
| $a_{ij}=\alpha$ |
| for $j=j+1,\cdots,n$ |
| $\alpha=a_{ij}$ |
| for $p=1,\cdots,i-1$ |
| $\alpha=\alpha-a_{jp}a_{pi}$ |
| $a_{ji}=\displaystyle\frac{\alpha}{a_{jj}}$ |
Figure 2 depicts the computational sequence associated with Crout’s method.
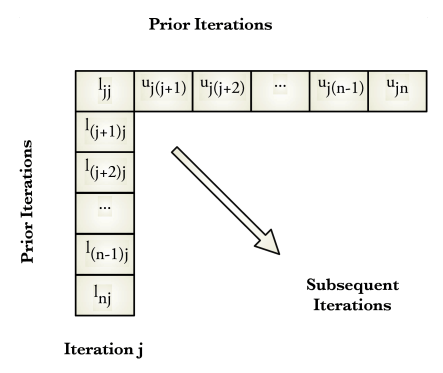
You should observe that Crout’s method, like Doolittle’s, exhibits inner product accumulation.
A good comparison of the various compact factorization
schemes is found in
Duff