4.4 LDU Factorization
Some factorization algorithms, referred to as LDU decompositions, derive three matrices L, D, and U from A such that
| $$\mathbf{LDU=A}$$ | (51) |
where L is unit upper triangular, D is diagonal, and U is unit lower triangular. It should be obvious that the storage requirements of LDU decompositions and LU decompositions are the same.
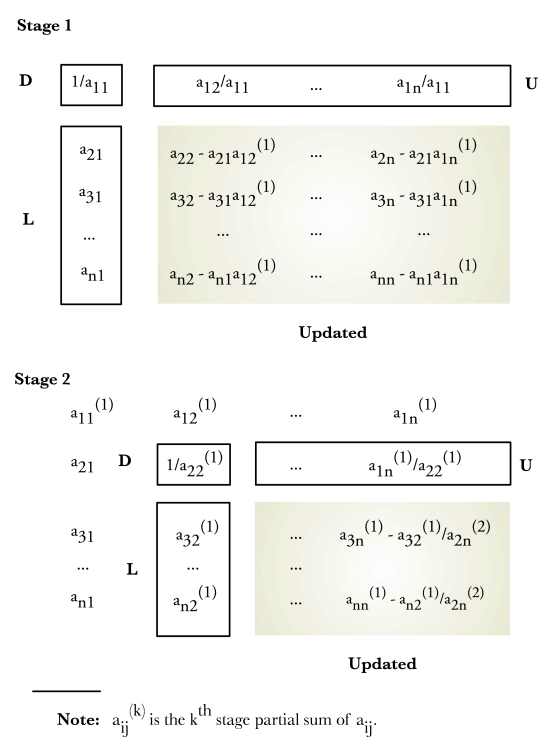
A procedure proposed by Tinnney and Walker[6] provides a concrete example of an LDU decomposition that is based on Gaussian elimination. One row of the subdiagonal portion of A is eliminated at each stage of the computation. Tinney refers to the LDU decomposition as a “table of factors”. He constructs the factorization as follows:
-
The elements of the unit upper triangular matrix U are $u_{ij}=a_{ij}^{(i)}$, where i < j.
-
The elements of the diagonal matrix D are $d_{ii}=\frac{1}{a_{ii}^{(i-l)}}$.
-
The elements of the unit lower triangular matrix L are $l_{ij}=a_{ij}^{(j-1)}$, where i < j.
Figure 3 depicts the first two stages of Tinney’s factorization procedure.