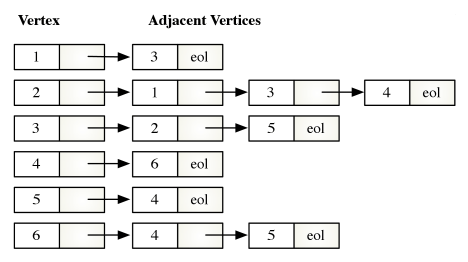
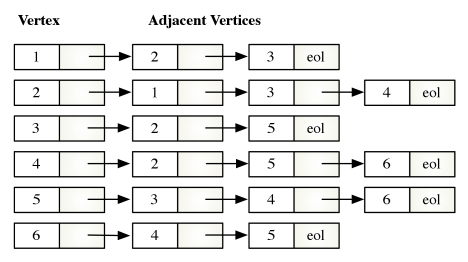
2.3 Representing Sparse Graphs as Adjaceny Lists

An adjacency list is a data structure for representing adjacency relationships in sparse graphs. The adjacency list of $G$ is actually a set of $|V|$ linked lists. Each vertex $v$ is the head of a list. Vertices adjacent to $v$ form the body of each list. If a vertex is not adjacent to any other vertices its list is empty.

The storage required to implement an adjacency list is proportional to $|V|+|E|$. When $G$ is represented as an adjacency list, the best time complexity you can expect for graph algorithms is $O\left(|V|+|E|\right)$. The time required to access each vertex and each edge exactly one time. An algorithm whose time complexity is $O\left(|V|+|E|\right)$ is sometimes referred to as linear in the size of $G$.

Figure 7 depicts the adjacency list for the directed graph in Figure 1.

Figure 8 depicts the adjacency list for the undirected graph in Figure 2.