1.2 Directed Graph
If the edges of are ordered pairs, then is a directed graph. In a directed graph, .
A directed graph is often referred to as a digraph. If edge of a digraph is represented by , then is an edge from to . Vertex is adjacent to vertex . Vertex is not adjacent to vertex unless the edge also exists in . The number of vertices adjacent to vertex is the degree of . In-degree indicates the number of edges incident upon . Out-degree indicates the number of edges emanating from .
Figure 1 depicts a directed graph with six vertices and ten edges. In the figure, the arrowheads indicate the direction of the edge.
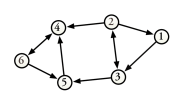
| Vertex | Degree | In-Degree | Out-Degree |
| 1 | 2 | 1 | 1 |
| 2 | 4 | 1 | 3 |
| 3 | 4 | 2 | 2 |
| 4 | 4 | 3 | 1 |
| 5 | 3 | 2 | 1 |
| 6 | 3 | 1 | 2 |