1.6 Acyclic Graph

A directed graph with no cycles is called directed acyclic graph or a DAG for short. An acyclic digraph has at least one vertex with an out-degree of zero.

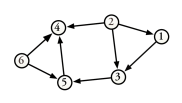
Figure 4 shows a variant of the directed graph of Figure 1 that contains no cycles. You will observe that vertex 4 has an out-degree of zero.

A directed tree is a connected DAG with the following properties:

• There is one vertex, called the root, which no edges enter.

• All vertices except the root have one entering edge.

• There is a unique path from each vertex to the root.

A DAG consisting of one or more trees is called a forest. If the graph $F=(V,E)$ is a forest and the edge $(v,w)$ is in $E(F)$, vertex $v$ is the parent of $w$ and vertex $w$ is the child of $v$. If there is a path from $v$ to $w$, then vertex $v$ is an ancestor of $w$ and vertex $w$ is a descendent of $v$. A vertex with no proper descendants is a leaf. A vertex $v$ and its descendants form a subtree of $F$. The vertex $v$ is the root of this subtree. The depth of vertex $v$ is the length of the path from the root to $v$. The height of vertex $v$ is the length of the longest path from $v$ to a leaf. The height of a tree is the height of its root. The level of vertex $v$ is its depth subtracted from the height of the tree.

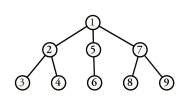
Figure 5 depicts a directed tree. Its root is vertex 1. Its leaves are the set of vertices $L(G)=\{ 3,4,6,8,9\}$.

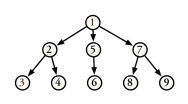
An undirected, connected, acyclic graph is called a free tree or an undirected tree. A rooted free tree is a free tree in which one vertex has been designated as the root. A directed tree is converted into a rooted free tree by discarding the orientation of the edges. A rooted free tree is converted into a directed tree by orienting each edge away from the root. The terminology which applies to directed trees also applies to rooted free trees.

Figure 6 depicts the directed tree of Figure 5 converted into a rooted free tree.