Transformer Model Transformer Model 2 Transformer Parameters

1 Transformer Equivalent Circuit

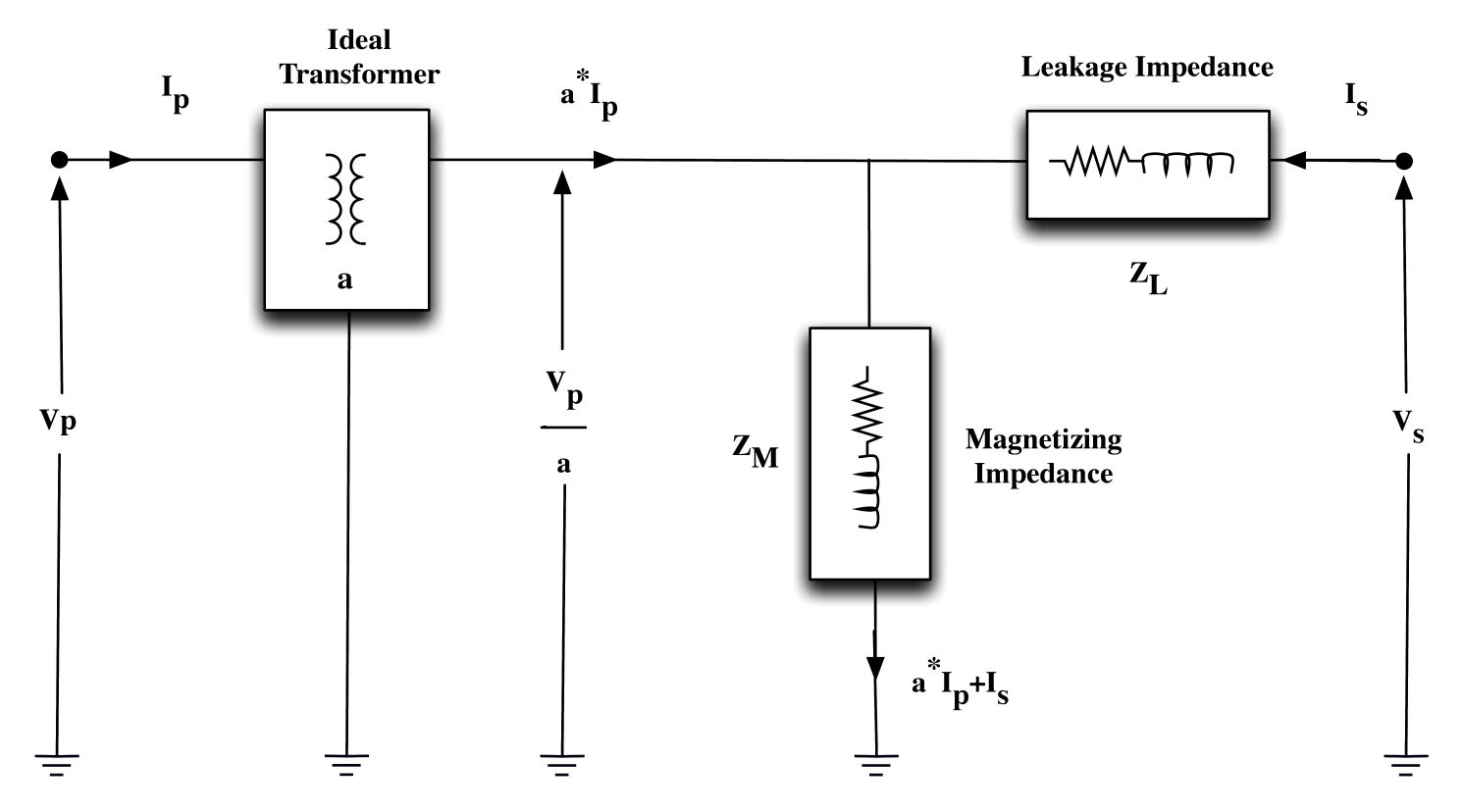
The equivalent circuit of a two winding transformer consists of an ideal transformer, a leakage impedance Z_L, and a magnetizing impedance Z_M. An ideal transformer is a lossless entity categorized by a complex voltage ratio a, i.e.

\mathbf{a=\frac{V_{p}}{V_{s}}}

(1)

where

V_p is the transformer’s primary voltage.

V_s is the transformer’s secondary voltage.

Since the ideal transformer has no losses, it must be true that

\mathbf{S_{p}=S_{s}}

(2)

\mathbf{V_{p}{I^{\star}_{p}}=V_{s}{I^{\star}_{s}}}

(3)

Solving for the secondary current

	$\displaystyle\mathbf{I^{\star}_{s}}$	$\displaystyle=\mathbf{\left(\frac{V_{p}}{V_{s}}\right){I^{\star}}_{p}}$		(4)
	$\displaystyle\mathbf{I_{s}}$	$\displaystyle=\mathbf{{\left(\frac{V_{p}}{V_{s}}\right)}^{\star}I_{p}}$		(5)

Substituting Equation 1 reveals the relationship between the primary and secondary current of an ideal transformer

\mathbf{I_{s}}=\mathbf{a^{\star}I_{p}}

(6)

where

I_p is current into the transformer’s primary.

I_s is current out of the transformer’s secondary.

a is the transformer’s voltage transformation ratio.

A transformer’s magnetizing impedance is a shunt element associated with its excitation current, i.e. the “no load” current in the primary windings. The real component of the magnetizing impedance reflects the core losses of the transformer. Its reactive component describes the mmf required to overcome the magnetic reluctance of the core.

A transformer’s leakage impedance is a series element that reflects imperfections in the windings. The real component of the leakage impedance is the resistance of the windings. Its reactive component is due to leakage flux, i.e. flux in the magnetic circuit that does not contribute to coupling the windings.

Figure 1 depicts a transformer’s equivalent circuit with impedances referred to the secondary.

Figure 1: Transformer Equivalent Circuit Diagram

Diagram of the equivalent circuit of a two winding transformer consisting of an ideal transformer, a leakage impedance, and a magnetizing impedance.